Решение нестандартных геометрических задач

Автор: Артамонова Станислава Антоновна

Организация: МБОУ СОШ №4

Населенный пункт: Ханты-Мансийский автономный округ - Югра, г. Пыть Ях

    В данной статье, исходя из экспериментальной работы, проведенной в IX-XI классах, показано, как можно организовать на уроке подготовку к решению нестандартных задач по геометрии. Практика показывает, что идея доказательства усваива­ется учащимися очень непросто. В ГИА 2017г 16% участников выполнили задачу на простейшее геометрическое доказательство. Как показывают результаты ЕГЭ, за решение геометрических задач №16 берётся низкий процент выпускников, что свидетельствует о трудности восприятия условия таких задач. Типична ситуация, когда даже хороший учащийся имитирует некоторые приемы, не понимая сути той всеобщности, логической ограниченности допустимых средств, которые лежат в основе идеи доказа­тельства.

   А. Н. Колмогоров высказал мысль о том, что в преподавании школьного курса геометрии можно выделить пять уровней. Готовить можно учащихся к решению таких задач, если они уже находятся на  третьем уровне предполагается усвоение учащимися формально-логической схемы геометрии, ее основных понятий, достаточного набора теорем и фактов, достаточно обширная практика в решении геометрических задач. Этот уровень можно охарактеризовать как уровень хорошего выпускника. На своих уроках если после изучения свойств параллелограмма предлагаю учащимся исследовать параллелограмм, и выдвинуть еще какие-нибудь его свойства, а затем их доказать.

  Четвертый уровень — это освоение курса школьной геометрии в его полном традиционном объеме. Предполагается, что на этом уровне учащийся владеет не только общими геометрическими фактами, но и специальной техникой решения геометрических задач (дополнительные построения, соображения размерности, подобия и т. п.). Геометрические задачи на экзамене вызывает трудности у многих обучающихся. Их решают плохо не только потом, что выпускники не знают или не могут использовать определенную теорему или формулу, но еще и потому, но ещё и потому, что они не могут описать решение задачи.  Большинство задач требует применения разнообразных теоретических знаний, доказательства утверждений, справедливых лишь при определенном расположении фигуры, применение различных формул. Особое внимание нужно уделить чертежу.  Он значительно облегчить решение задачи, если он соответствует, условию задачи то обучающийся, может увидеть путь решения задачи, который потом реализуется со ссылкой на чертеж.          

   Задачи, предложенные, на данном уроке ориентированы на повторения курса по геометрии и позволяет подготовиться, к решению геометрической задачи №16 по планиметрии профильного уровня ЕГЭ по математике действительно, считаются самыми трудными. Трудность у учащихся заключается в том, что на изучении планиметрии в обычной школе отводится только два урока в неделю. Эту дисциплину изучают в 7-9х классах, это мало времени для изучения плоских фигур и их свойств и научиться применять их при решении задач. Кроме того, каждая задача по геометрии уникальна по своему содержанию, поэтому для решения таких задач практически неприменим алгоритмический подход, который является весьма успешным при решении задач по алгебре, в результате многие школьники даже не пытаются решать геометрические задачи. Все это приводит к тому, что и сравнительно несложная задача по планиметрии становится непосильной для выпускников школ.  Ситуацию можно исправить, но потребуется немало сил и времени и, конечно, хорошая методика подготовки. Моя методика по решению геометрической задачи №16 по планиметрии профильного уровня ЕГЭ по математике основана на методики известного отечественного методолога и методиста, специалиста по преподаванию геометрии Р.К. Гордина. Суть его методики заключается в том, что в учебных материалах последовательно разбираются свойства геометрических фигур и их элементов начиная от прямоугольного треугольника и заканчивая дополнительными построения при решении геометрических задач повышенной сложности. Методы решения данных задач срабатывают и на олимпиадах по математике решения нестандартные задачи.

 Поиск средства разрешения противоречия приводит к формированию способа действия, последний позволяет решать целые классы задач.  В курсе геометрии выделяют следующие виды нестандартных задач:

–  на доказательство;

–  на построение;

–  на вычисление;

–  занимательные.

В чем же заключается нестандартность задач?  Для обучающегося,

который впервые встречается с задачей, требующей применения новой для

него идеи, задача является нестандартной. Приемы нестандартных дополнительных построении при решении геометрических задач:

1. Проведение прямой параллельной боковой стороне,
2. Удвоение медианы,
3. Проведение высот,
4. Проведение прямой параллельной диагонали,
5. Продолжение боковых сторон.

Конечно, все приведенные рекомендации имеют не всеобщий характер, и при решении отдельных геометрических задач чертеж фигур и краткая запись условия могут производиться иначе. Разумеется, невозможно перечислить все дополнительные построения, которые могут быть полезны при решении задач. В задачах, где участвует медиана треугольника, почти всегда бывает полезно ее удвоить, достроив до параллелограмма. В этом случае появляется возможность использовать также и свойства параллелограмма.

На данном уроке рассматриваются два приема решения нестандартных геометрических задач с помощью дополнительных построении. Сразу хочется оговорится, что этот урок проводился с подготовленными учащимися 9-х - 11-х классов.

1-й прием.   Проведение прямой параллельной боковой стороне

    Особое внимание нужно уделить чертежу, а дополнительные построения позволят значительно облегчить решение задачи. Или если в задаче в качестве основного объекта названа трапеция и не указан ее вид, то не следует строить равнобедренную или прямоугольную трапецию и т. д.

  При построении чертежа нет надобности выдерживать строго какой-либо определенный масштаб.  Однако желательно соблюдать какие-то пропорции в построении отдельных элементов фигуры. Например, если по условию задачи углы при большем основании трапеции равны 30◦ и 60◦, а отрезок, соединяющий середины оснований, равен 3.  то это должно быть соблюдено на чертеже.  Или если задана медиана треугольника, то соответствующий ей отрезок на чертеже должен проходить приблизительно через середину стороны трапеции и т. д. параллельность, перпендикулярность и другие, заданные в задаче параметры.  Данный прием позволяет нам провести через данную точку М прямые, параллельные боковым сторонам трапеции, получим прямой угол РМQ.  В свою очередь параллельность сторон дает возможность применить признак параллельности прямых и указать на равенство соответственных углов. Таким образом, мы уже работаем с прямоугольным треугольником, что позволяет применить его свойства. Обучающийся может увидеть уже знакомый путь решения задачи, который потом реализуется со ссылкой на чертеж.

1.15. Средняя линия трапеции равна 5, а отрезок, соединяющий середины оснований, равен 3. Углы при большем основании трапеции равны 30◦ и 60◦. Найдите основания и меньшую боковую сторону трапеции

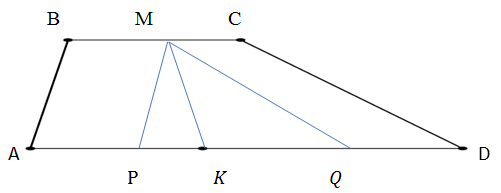
Решение.

 Через середину M меньшего основания BC трапеции ABCD проведём прямую, параллельную боковой стороне AB, до пересечения с основанием AD в точке P и прямую, параллельную боковой стороне CD, до пересечения с прямой AD в точке Q.   Если K —середина AD, то PK = AK − AP = AK −BM = DK −MC = DK −QD = KQ, поэтому MK —медиана треугольника PMQ, а т. к. ∠PMQ = 180◦ −60◦ −30◦ = 90◦, то PK =KQ=MK =3. Значит, AD−BC = PQ = 6, AD+BC = 10, откуда находим, что AD=8 и BC =2. Пусть PM —катет прямоугольного треугольника PMQ, лежащий

против угла в 30◦. Тогда AB—меньшая боковая сторона трапеции ABCD и AB = PM =12   PQ = 3.

Ответ: 8; 2; 3.

2-й прием

Удвоение медианы

 

В задачах, где участвует медиана треугольника, почти всегда бывает полезно ее удвоить, достроив до параллелограмма. В этом случае появляется возможность использовать также и свойства параллелограмма.

2.16.    Найдите площадь треугольника, если две его стороны равны

27 и 29, а медиана, проведённая к третьей, равна 26.

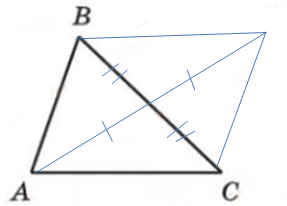
 Решение.

Пусть стороны AB и BC треугольника ABC равны соответственно 27 и 29, а его медиана BM равна 26. На продолжении медианы BM за точку M отложим отрезок MD, равный BM. Из равенства треугольников ABM и CDM следует равенство

площадей треугольников ABC и BCD. В треугольнике BCD известно,

что BC = 29, BD = 2BM = 52, DC = AB = 27.

По формуле Герона

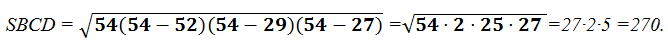
Следовательно,

SABC = SBCD = 270.

                                                   

                            Ответ: 270.

Конечно, для решения геометрических задач большое значение имеет хорошее знание теории, поэтому в наших материалах много кратких видеолекций, суммирующих необходимые теоретические знания. Обучая теории, мы сразу же разбираем опорные задачи, в которых она применяется, осваиваем специальные приемы решения задач – например метод проекций, метод площадей, метод вспомогательной окружности и т. д.  После изучения теории нужно браться за самостоятельное решение задач. При этом можно выбрать приемлемую траекторию продвижения по системе задач. Для менее подготовленных школьников мы рекомендуем решать задачи «по фигурам», то есть в следующем порядке. Сначала – прямоугольный треугольник, медиана в прямоугольном треугольнике, биссектриса в прямоугольном треугольнике, высота в прямоугольном треугольнике. Затем переходим к равнобедренному и произвольному треугольникам, параллелограмму, трапеции и т. д. Для более сильных школьников предлагается другой путь – систематизация и обобщение свойств геометрических фигур и их элементов. Прямоугольный треугольник, произвольный треугольник (теорема синусов, теорема косинусов, площади), медиана в прямоугольном треугольнике, медиана в равнобедренном и произвольном треугольнике и т. д. Описанный подход позволяет нашим ученикам актуализировать свои школьные знания, обобщить и углубить их, систематически сочетая изучение теории с практикой ее применения. Большую помощь в решении задач оказывают пошаговые тренажеры: в геометрической задаче, ход решения которой может быть неочевиден с самого начала, тренажер позволяет сориентироваться в шагах решения, проверить промежуточные вычисления на каждом шаге и обосновать сами шаги нужной теоремой или свойством. После такой подготовки задачи по планиметрии варианта КИМ ЕГЭ покажутся и не такими уж сложными. Посмотрим, например, как можно «раскусить» следующую довольно непростую, но в то же время изящную задачу, предлагавшуюся на экзамене в 2016–2017 годах.

 

Литература:

Интернет-ресурсы:

1.Гордин Р.К.  ЕГЭ 2017. Математика. Решение задачи 16 (профильный уровень).—М.: МЦНМО, 2017.—448 с. ISBN 978-5-4439-1090-1

2. Гордин Р. К. Геометрия. Планиметрия. 7—9 классы. М.: МЦНМО, 2014.

3. Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Планиметрия. Задача 16 (профильный уровень). М.: МЦНМО, 2017.

4. Гордин Р. К. Теоремы и задачи школьной геометрии. Базовый и профильный уровни. М.: МЦНМО, 2015

5.Математика:  справочник  формул  по  алгебре  и  геометрии,  решения задач  и  примеров.  Математические  формулы  on-line  [Электронный

ресурс]. - Режим доступа : http://www.pm298.ru, свободный. -  Загл. с экрана.

1. file0.docx.. 75,9 КБ

Опубликовано: 09.11.2021